B样条曲线
1.B样条曲线基础知识
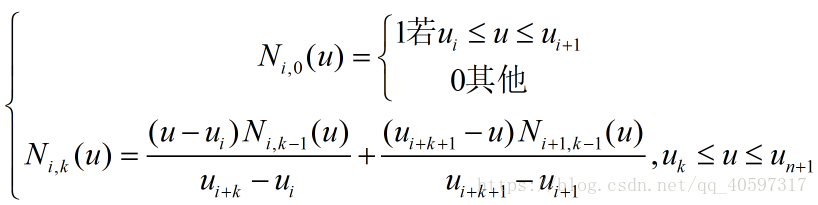
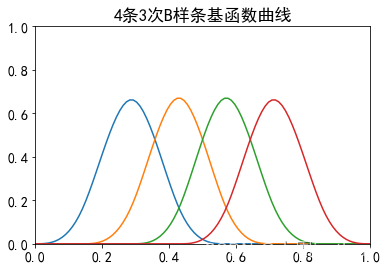
对一个次数一定的B样条曲线来说,其每一个控制点前的基函数可以看作是同一个基函数平移得到的,如下图所示。因此,对一个次数确定的B样条曲线,关键便是求解其在作用域空间内的一个基函数。
2.B样条曲线点坐标的求解
在获得目标点坐标的前提下,B样条曲线上各个节点的坐标可以用如下表达式确立:
其中的m为对应点坐标在该区段上基函数的分段表达式,P为点的坐标。因此,求解曲线上点坐标的关键便是求解对应的基函数。基函数的非零作用域为[i, i+k+1],因此,对于B样条曲线来说,在两个节点之间,能够影响该段的控制点数目为k+1个。
关于基函数的求解,可以参考文档,最终的坐标点求解方程可以表示为:
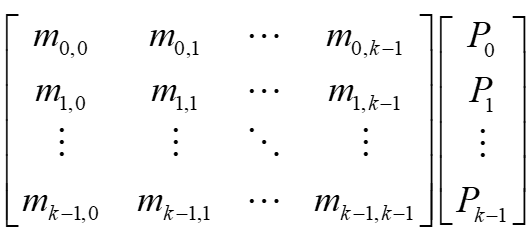

3.B样条曲线导数的求解
B样条曲线的导数公式如下,其可以表示成上一阶M矩阵的形式,因此B样条曲线的导数还可以由更低阶的B样条曲线表示,具体形式如下:

4.基于B样条曲线的参考路径优化问题建立
针对B样条曲线,优化的目标包括以下几点:
- 路径与原始路径的偏差deviation
- 路径上曲线对参数t的二阶导数,可以理解为曲线上的加速度a
- 路径上曲线对参数t的三阶导数,可以理解为jerk
- 路径上曲线对参数t的四阶导数,可以理解为snap
优化的约束设置为:
- 当t=0时,B样条曲线经过该线段的第一个点
因此,该优化问题可以建模为如下二次规划问题:
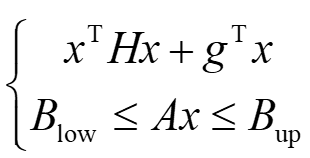
针对路径与原始路径的偏差deviation,由于原始控制点是由原始路径点通过插值反运算求解得到的,因此当原始控制点不变时,原始路径不变,原始路径的偏离程度可以理解为控制点的偏移程度,可以得到如下H矩阵和g向量。
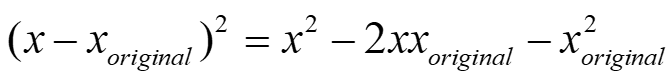
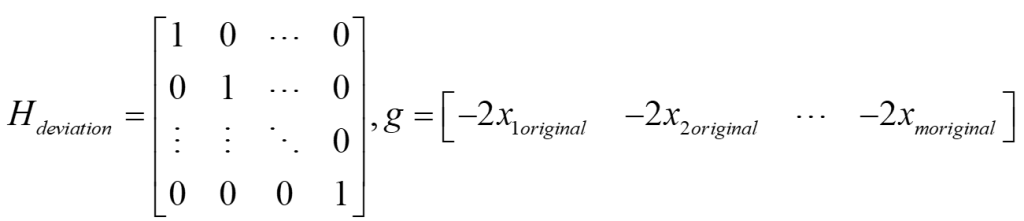
针对路径上的二阶导数,由之前关于B样条曲线中的导数推论可以得到:其中D矩阵为之前求导公式中由-1和1组成的矩阵。
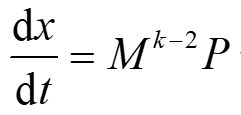
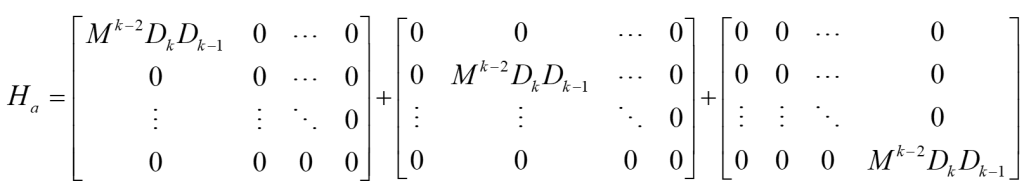
类似的,针对三阶和四阶导数,可以得到
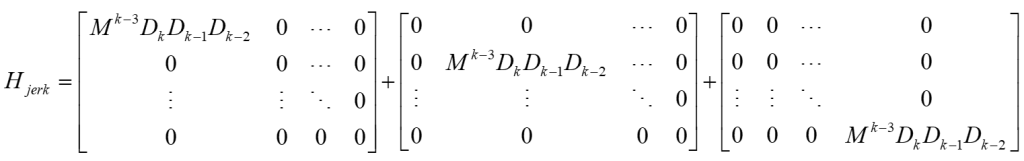

至此,可以得到二次优化问题的优化目标:
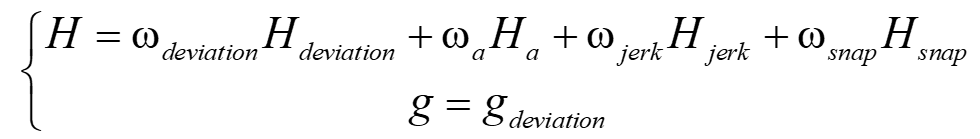
对于约束条件,则单纯定为在经过指定节点
5.B样条曲线避障问题问题建立
B样条曲线中的避障问题建立,其主要可以分为如下步骤:
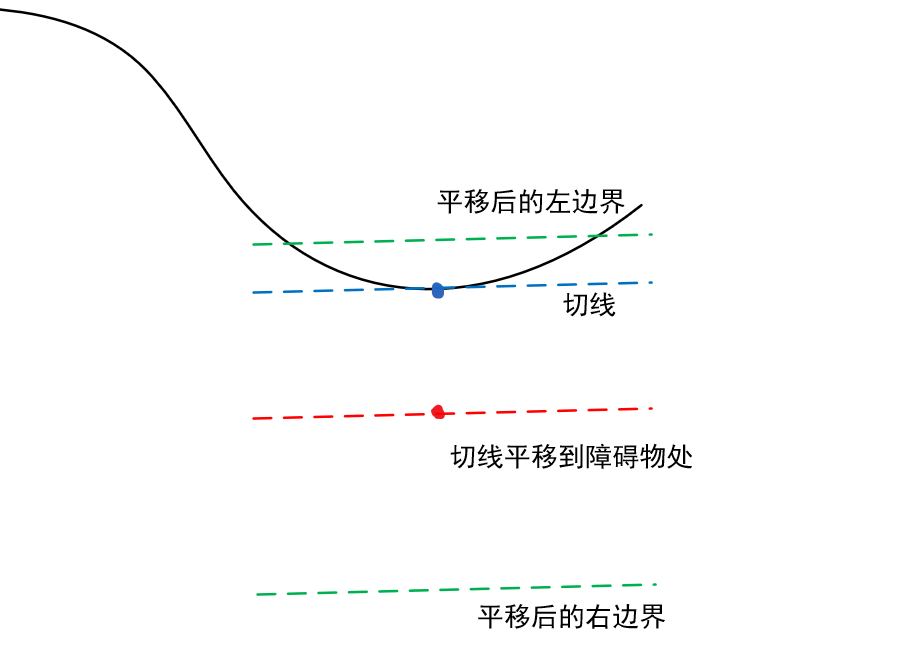
1. 找到曲线上距离障碍物最近的点,以及其对应的参数t。
2. 找到该点处的切线方程。
3.根据决策模块的左右避障指令来建立约束,约束条件为切线向两侧偏移一定距离。
下图中的顺序依次是:蓝-红-绿